PHPSimplex

Exemple (partie 2): méthode Graphique

Résoudre moyennant la méthode Graphique le prochain problème:

Maximiser	Z = f(x,y) = 3x + 2y
sous les contraintes:	2x + y ≤ 18
	2x + 3y ≤ 42
	3x + y ≤ 24
	x ≥ 0 , y ≥ 0

1. D'abord, on trace le système de coordonnées. On représente la variable "x" en abscisse et "y" en ordonnée, qu'on montre dans cette figure.
2. On divise numériquement les axes selon les valeurs que les variables peuvent avoir par rapport aux contraintes du problème. Pour ce faire, dans chaque contrainte il faut faire nuls toutes les variables hormis la correspondante à un axe en particulier, établissant la valeur correcte pour cet axe. On répète ce processus dans chacun des axes.
3. Ensuite, on représente les contraintes. On commence par la première, on trace la droite qu'on obtient si on considère la contrainte comme égale. Elle apparaît comme le segment qui met en relation A et B, cette région délimité c'est en couleur JAUNE. On reproduit le processus avec les autres contraintes, donnant pour résultat la région en couleur BLEU et ROUGE pour la deuxième et troisième contrainte respectivement.
4. La région réalisable est l'intersection des régions délimitées aussi par l'ensemble des contraintes, que par les conditions de non-négativé des variables, c'est-à-dire, par les deux axes de coordonnés. Cette région est représentée par le polygone O-F-H-G-C, en couleur VIOLET.
   
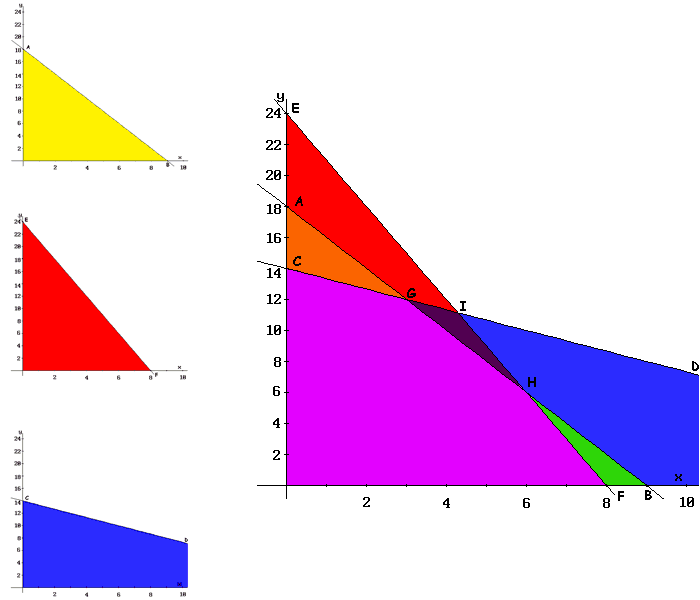
5. Puisqu'il y a une région réalisable, on détermine les points dans l'extrémité, ou les sommets du polygone qui représente. Ces sommets sont les points candidats à solutions optimales. Dans cet exemple ils sont les points O-F-H-G-C de la figure.
6. Finalement, on évalue la fonction objectif (3x + 2y) dans chacun des points (résultat qu'on recueilli dans le tableau suivant). Comme le point G fournit la plus grande valeur à la fonction Z et l'objectif c'est de maximiser, ce point représente la solution optimale: Z = 33 avec x = 3 et y = 12.

Sommet	Coordonnées (x,y)	Valeur objectif (Z)
O	(0,0)	0
C	(0,14)	28
G	(3,12)	33
H	(6,6)	30
F	(8,0)	24

Comparaison de la méthode Graphique avec la méthode du Simplexe

Les successifs tableaux construits au fil de la méthode du Simplexe fournissent la valeur de la fonction objectif des différents sommets de la région réalisable, qui au même temps s'adapte aux coefficients des variables initiaux et d'écart.

Dans le tableau initial on a calculé la valeur de la fonction objectif dans le sommet O, dont les coordonnées (0,0) correspondent avec la valeur que les variables basiques ont, ayant un résultat 0.

Tableau I . Itération 1ère
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	18	2	1	1	0	0
P4	0	42	2	3	0	1	0
P5	0	24	3	1	0	0	1
Z		0	-3	-2	0	0	0

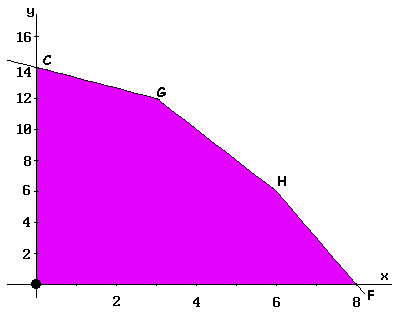
La variable qui entre dans la base de la méthode du Simplexe détermine vers quel nouveau sommet on fait le déplacement. Dans cet exemple, comme P1 entre (correspondant à 'x'), le déplacement se produit par l'arête OF jusqu'arriver au sommet F, où on calcule la valeur que la fonction Z prend. Cette étape a lieu dans la deuxième itération de la méthode du Simplexe, montrée dans le Tableau II. Dans lui, on a établi la valeur qui correspond au sommet F en ayant une valeur Z = 24 pour la fonction.

Tableau II . Itération 2ème
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	2	0	1/3	1	0	-2/3
P4	0	26	0	7/3	0	1	-2/3
P1	3	8	1	1/3	0	0	1/3
Z		24	0	-1	0	0	1

On fait un nouveau déplacement par l'arête FH, jusqu'arriver à H (données dans le Tableau III). Dans cette troisième itération on calcule la valeur de la fonction dans le sommet H, en s'obtenant Z = 30.

Tableau III . Itération 3ème
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	6	0	1	3	0	-2
P4	0	12	0	0	-7	1	4
P1	3	6	1	0	-1	0	1
Z		30	0	0	3	0	-1

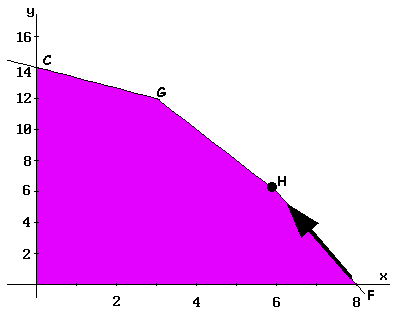
On continue avec le processus à travers de l'arête HG, jusqu'à le sommet G. Les données obtenues se révèlent dans le Tableau IV. Dans ce point le processus prend terme, on peut vérifier que la solution n'améliore pas si l'on déplace par l'arête GC jusqu'au sommet C (ne surpasse pas la valeur actuelle de la fonction).

Tableau IV . Itération 4ème
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	12	0	1	-1/2	1/2	0
P5	0	3	0	0	-7/4	1/4	1
P1	3	3	1	0	3/4	-1/4	0
Z		33	0	0	5/4	1/4	0

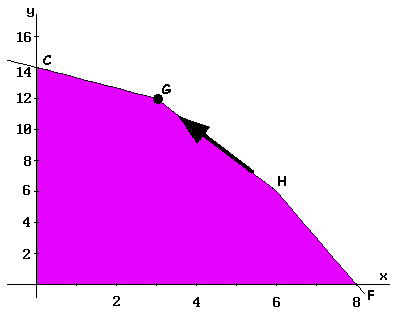
La valeur maximale de la fonction objectif c'est 33, correspondante aux valeurs x = 3 et y = 12 (coordonnées du sommet G).

Avec la méthode Graphique est nécessaire calculer la valeur de la fonction objectif dans tous les sommets de la région réalisable, alors qu'avec la méthode du Simplexe on finit quand on trouve la valeur optimale.

Résoudre avec PHPSimplex: méthode du Simplexe.

Résoudre avec PHPSimplex: méthode Graphique.