PHPSimplex

Optimizando recursos con Programación Lineal

Twittear

Ejemplo (parte 2): método Gráfico

Resolver mediante el método Gráfico el siguiente problema:

Maximizar	Z = f(x,y) = 3x + 2y
sujeto a:	2x + y ≤ 18
	2x + 3y ≤ 42
	3x + y ≤ 24
	x ≥ 0 , y ≥ 0

1. Inicialmente se dibuja el sistema de coordenadas asociando a un eje la variable "x" y al otro la "y" (generalmente se asocia 'x' al eje horizontal e 'y' al vertical), como se puede ver en la figura.
2. Se marca en dichos ejes una escala numérica apropiada a los valores que pueden tomar las variables de acuerdo a las restricciones del problema. Para ello en cada restricción se hacen nulas todas las variables excepto la correspondiente a un eje concreto, determinándose así el valor adecuado para dicho eje. Este proceso se repite para cada uno de los ejes.
3. A continuación se representan las restricciones. Comenzando con la primera, se dibuja la recta que se obtiene al considerar la restricción como igualdad. Aparece representada como el segmento que une A con B y la región que delimita ésta restricción viene indicada por el color AMARILLO. Se repite el proceso con las demás restricciones, quedando delimitadas la región de color AZUL y ROJO para la segunda y tercera restricción respectivamente.
4. La región factible es la intersección de las regiones delimitadas tanto por el conjunto de restricciones, como por las condiciones de no negatividad de las variables, es decir, por ambos ejes de coordenadas. Dicha región factible está representada por el polígono O-F-H-G-C, de color VIOLETA.
   
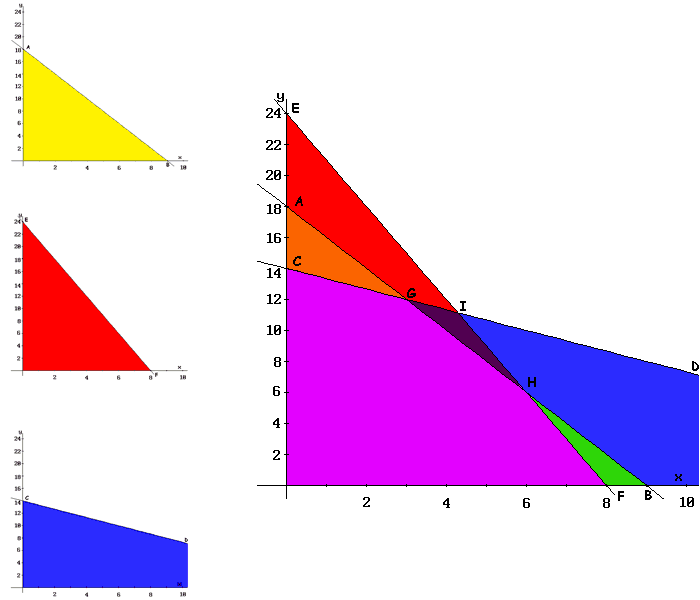
5. Como existe una región factible, se procede a determinar sus puntos extremos, o vértices del polígono que representa. Estos vértices son los puntos candidatos a soluciones óptimas. En este ejemplo son los puntos O-F-H-G-C de la figura.
6. Finalmente, se evalúa la función objetivo (3x + 2y) en cada uno de esos puntos (resultado que se recoge en la tabla siguiente). Como el punto G proporciona el mayor valor a la función Z y el objetivo es maximizar, tal punto constituye la solución óptima: Z = 33 con x = 3 e y = 12.

Punto extremo	Coordenadas (x,y)	Valor objetivo (Z)
O	(0,0)	0
C	(0,14)	28
G	(3,12)	33
H	(6,6)	30
F	(8,0)	24

Comparación del método Gráfico y el método Simplex

Las sucesivas tablas construidas durante el método Simplex van proporcionando el valor de la función objetivo en los distintos vértices de la región factible, ajustándose, a la vez, los coeficientes de las variables iniciales y de holgura.

En la tabla inicial se ha calculado el valor de la función objetivo en el vértice O, cuyas coordenadas (0,0) se corresponden con el valor que tienen las variables básicas, siendo el resultado 0.

Tabla I . Iteración nº 1
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	18	2	1	1	0	0
P4	0	42	2	3	0	1	0
P5	0	24	3	1	0	0	1
Z		0	-3	-2	0	0	0

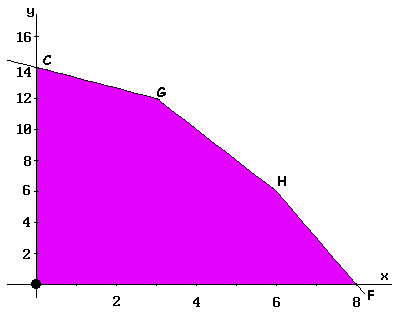
La variable que entra a la base en el método Simplex determina hacia qué nuevo vértice se realiza el desplazamiento. En este ejemplo, como entra P1 (correspondiente a 'x'), el desplazamiento se lleva a cabo por la arista OF hasta llegar al vértice F, donde se calcula el valor que toma la función Z. Este paso se produce en la segunda iteración del método Simplex, mostrado en la Tabla II. En ella se ha calculado el valor que corresponde al vértice F obteniéndose un valor Z = 24 para la función.

Tabla II . Iteración nº 2
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	2	0	1/3	1	0	-2/3
P4	0	26	0	7/3	0	1	-2/3
P1	3	8	1	1/3	0	0	1/3
Z		24	0	-1	0	0	1

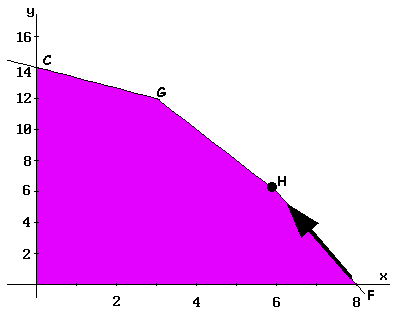
Se realiza un nuevo desplazamiento por la arista FH, hasta llegar a H (datos en la Tabla III). En esta tercera iteración se calcula el valor de la función en el vértice H, obteniéndose Z = 30.

Tabla III . Iteración nº 3
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	6	0	1	3	0	-2
P4	0	12	0	0	-7	1	4
P1	3	6	1	0	-1	0	1
Z		30	0	0	3	0	-1

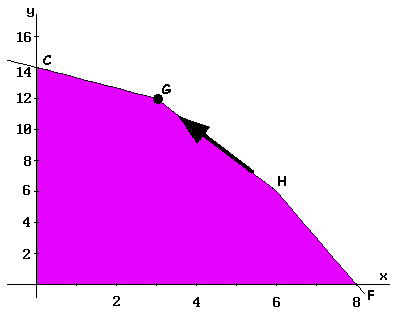
Se continúa el proceso a través de la arista HG, hasta llegar al vértice G. Los datos obtenidos se reflejan en la Tabla IV. En este punto acaba el proceso, pudiéndose comprobar que la solución no mejora al desplazarse por la arista GC hasta el vértice C (no supera el valor actual de la función).

Tabla IV . Iteración nº 4
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	12	0	1	-1/2	1/2	0
P5	0	3	0	0	-7/4	1/4	1
P1	3	3	1	0	3/4	-1/4	0
Z		33	0	0	5/4	1/4	0

El valor máximo de la función objetivo es 33, y corresponde a los valores x = 3 e y = 12 (coordenadas del vértice G).

Con el método Gráfico es necesario calcular el valor de la función objetivo en todos los vértices de le región factible, mientras que el método Simplex acaba en cuanto halla el valor óptimo.

Resolver con PHPSimplex: método Simplex.

Resolver con PHPSimplex: método Gráfico.

Copyright ©2006-2024 PHPSimplex. Todos los derechos reservados. Términos y condiciones.

X