PHPSimplex

Camino mínimo

Los problemas conocidos como problemas del camino mínimo o camino más corto tratan, como su nombre indica, de hallar la ruta mínima o más corta entre dos puntos. Este mínimo puede ser la distancia entre los puntos origen y destino o bien el tiempo transcurrido para trasladarse desde un punto a otro. Se aplica mucho para problemas de redes de comunicaciones.

Este tipo de problemas pueden ser resueltos por el método del Simplex, sin embargo existen otros métodos más eficientes como por ejemplo el algoritmo de Dijkstra o el de Bellman-Ford.

Ejemplo

Una persona tiene que desplazarse a diario de un pueblo A a otro G. Está estudiando cual es el trayecto más corto usando un mapa de carreteras. Las carreteras y sus distancias están representadas en la figura siguiente:

 

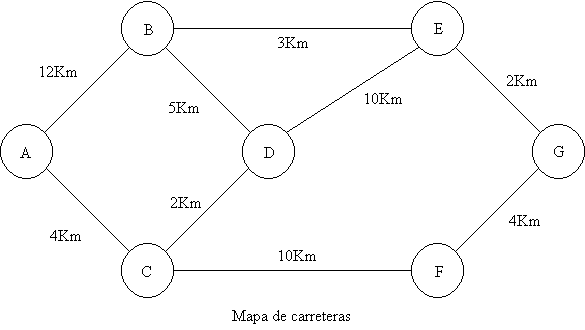
Determinar las variables de decisión y expresarlas algebraicamente. En este caso:

• Xij: acción de desplazarse del pueblo i al j (0 indica que no hay desplazamiento y 1 que sí hay desplazamiento)

Determinar las restricciones y expresarlas como ecuaciones o inecuaciones dependientes de las variables de decisión. Dichas restricciones se deducen del balance entre los posibles caminos que parten desde cada pueblo y los que llegan hasta él (obviando los caminos que regresen al punto de partida y aquellos que provengan del punto de destino):

• Balance de caminos del pueblo A: XAB + XAC = 1
• Balance de caminos del pueblo B: XBD + XBE - XAB - XDB - XEB = 0
• Balance de caminos del pueblo C: XCD + XCF - XAC - XDC - XFC = 0
• Balance de caminos del pueblo D: XDB + XDC + XDE - XBD - XCD - XED = 0
• Balance de caminos del pueblo E: XEB + XED + XEG - XBE - XDE = 0
• Balance de caminos del pueblo F: XFC + XFG - XCF = 0
• Balance de caminos del pueblo G: - XEG - XFG = -1

Expresar todas las condiciones implícitamente establecidas por la naturaleza de las variables: que no puedan ser negativas, que sean enteras, que solo puedan tomar determinados valores, ... En este caso las restricciones son que las variables deben ser booleanas (0 no se toma el camino, 1 se toma), y por lo tanto no pueden ser negativas:

• Xij ≥ 0
• Xij es booleano

Determinar la función objetivo:

• Minimizar Z = 12·XAB + 4·XAC + 5·XBD + 3·XBE + 2·XCD + 10·XCF + 5·XDB + 2·XDC + 10·XDE + 3·XEB + 10·XED + 2·XEG + 10·XFC + 4·XFG

Realizar un cambio de variables con la siguiente correspondencia:

XAB

XAC

XBE

XBD

XDB

XEB

XCD

XCF

XFC

XDC

XDE

XED

XEG

XFG

X1

X2

X3

X4

X5

X6

X7

X8

X9

X10

X11

X12

X13

X14

Resolver con PHPSimplex.