PHPSimplex

Optimizando recursos con Programación Lineal

Teoría del método Simplex

El método Simplex es un procedimiento iterativo que permite mejorar la solución de la función objetivo en cada paso. El proceso concluye cuando no es posible continuar mejorando dicho valor, es decir, se ha alcanzado la solución óptima (el mayor o menor valor posible, según el caso, para el que se satisfacen todas las restricciones).

Partiendo del valor de la función objetivo en un punto cualquiera, el procedimiento consiste en buscar otro punto que mejore el valor anterior. Como se verá en el método Gráfico, dichos puntos son los vértices del polígono (o poliedro o polícoro, si el número de variables es mayor de 2) que constituye la región determinada por las restricciones a las que se encuentra sujeto el problema (llamada región factible). La búsqueda se realiza mediante desplazamientos por las aristas del polígono, desde el vértice actual hasta uno adyacente que mejore el valor de la función objetivo. Siempre que exista región factible, como su número de vértices y de aristas es finito, será posible encontrar la solución.

El método Simplex se basa en la siguiente propiedad: si la función objetivo Z no toma su valor máximo en el vértice A, entonces existe una arista que parte de A y a lo largo de la cual el valor de Z aumenta.

Será necesario tener en cuenta que el método Simplex únicamente trabaja con restricciones del problema cuyas inecuaciones sean del tipo "≤" (menor o igual) y sus coeficientes independientes sean mayores o iguales a 0. Por tanto habrá que estandarizar las restricciones para que cumplan estos requisitos antes de iniciar el algoritmo del Simplex. En caso de que después de éste proceso aparezcan restricciones del tipo "≥" (mayor o igual) o "=" (igualdad), o no se puedan cambiar, será necesario emplear otros métodos de resolución, siendo el más común el método de las Dos Fases.

Preparando el modelo para adaptarlo al método Simplex

La forma estándar del modelo de problema consta de una función objetivo sujeta a determinadas restricciones:

Función objetivo:	c1·x1 + c2·x2 + ... + cn·xn
Sujeto a:	a11·x1 + a12·x2 + ... + a1n·xn = b1 a21·x1 + a22·x2 + ... + a2n·xn = b2 ... am1·x1 + am2·x2 + ... + amn·xn = bm x1,..., xn ≥ 0

El modelo debe cumplir las siguientes condiciones:

El objetivo consistirá en maximizar o minimizar el valor de la función objetivo (por ejemplo, incrementar ganancias o reducir pérdidas, respectivamente).
Todas las restricciones deben ser ecuaciones de igualdad (identidades matemáticas).
Todas las variables (xi) deben tener valor positivo o nulo (condición de no negatividad).
Los términos independientes (bi) de cada ecuación deben ser no negativos.

Hay que adaptar el problema modelado a la forma estándar para poder aplicar el algoritmo del Simplex.

Tipo de optimización.

Como se ha comentado, el objetivo del método consistirá en optimizar el valor de la función objetivo. Sin embargo se presentan dos opciones: obtener el valor óptimo mayor (maximizar) u obtener el valor óptimo menor (minimizar).

Además existen diferencias en el algoritmo entre el objetivo de maximización y el de minimización en cuanto al criterio de condición de parada para finalizar las iteraciones y a las condiciones de entrada y salida de la base. Así:

Objetivo de maximización
Condición de parada: cuando en la fila Z no aparece ningún valor negativo.

Condición de entrada a la base: el menor valor negativo en la fila Z (o el de mayor valor absoluto entre los negativos) indica la variable Pj que entra a la base.

Condición de salida de la base: una vez obtenida la variable entrante, la variable que sale se determina mediante el menor cociente P0/Pj de los estrictamente positivos.
Objetivo de minimización
Condición de parada: cuando en la fila Z no aparece ningún valor positivo.

Condición de entrada a la base: el mayor valor positivo en la fila Z indica la variable Pj que entra a la base.

Condición de salida de la base: una vez obtenida la variable entrante, la variable que sale se determina mediante el menor cociente P0/Pj de los estrictamente negativos.

No obstante, es posible normalizar el objetivo del problema con el fin de aplicar siempre los mismos criterios en lo referente a la condición de parada del algoritmo y a las condiciones de entrada y salida de las variables de la base. De esta forma, si el objetivo es minimizar la solución, se puede cambiar el problema a otro equivalente de maximización simplemente multiplicando la función objetivo por "-1". Es decir, el problema de minimizar Z es equivalente al problema de maximizar (-1)·Z. Una vez obtenida la solución será necesario multiplicarla también por (-1).

Ventajas: No hay que preocuparse por nuevos criterios de parada, condición de entrada y salida de la base ya que se mantienen.

Inconvenientes: En el caso de que la función tenga todos los coeficientes de sus variables básicas positivos, y además las restricciones sean del tipo de desigualdad "≤", al hacer el cambio dichos coeficientes quedan negativos cumpliéndose la condición de parada en la primera iteración (en la fila del valor de la función objetivo todos los valores son positivos o cero). Obteniéndose en este caso por defecto un valor óptimo para la función igual a 0.

Solución: Realmente no existe este problema dado que para que la solución sea superior a 0 es necesario que alguna restricción tenga impuesta la condición "≥" (y se trataría de un modelo para el método de las Dos Fases). En el caso planteado, la solución real debe ser cero.

Cambio de signo de los términos independientes

También se ha dicho que los términos independientes (bi) de cada ecuación deben ser no negativos para poder emplear el método Simplex. A tal fin, si alguna de las restricciones presenta un término independiente menor que 0 habrá que multiplicar por "-1" ambos lados de la inecuación (teniendo en cuenta que esta operación también afecta al tipo de restricción).

Ventajas: Con ésta simple modificación de signos en las restricciones correspondientes se posibilita la aplicación del método Simplex al problema modelado.

Inconvenientes: Puede resultar que en las restricciones donde tengamos que modificar los signos de las constantes, los tipos de desigualdad fueran "≤" (quedando tras la operación del tipo "≥") siendo necesario desarrollar el método de las Dos Fases. Este inconveniente no es controlable, aunque podría ocurrir el caso contrario y resultar beneficioso si los términos independientes negativos se presentan en todas aquellas restricciones con desigualdad de tipo "≥". Si existe alguna restricción del tipo "=" no supondría ninguna ventaja ni desventaja puesto que siempre sería de necesaria aplicación el método de las Dos Fases.

Normalización de las restricciones

Otra de las condiciones del modelo estándar del problema es que todas las restricciones sean ecuaciones de igualdad (también llamadas restricciones de igualdad), por lo que hay que convertir las restricciones de desigualdad o inecuaciones en dichas identidades matemáticas.

La condición de no negatividad de las variables (x1,..., xn ≥ 0) es la única excepción y se mantiene tal cual.

Restricción de tipo "≤"
Para normalizar una restricción con una desigualdad del tipo "≤", hay que añadir una nueva variable, llamada variable de holgura xs (con la condición de no negatividad: xs ≥ 0). Esta nueva variable aparece con coeficiente cero en la función objetivo, y sumando en la ecuación correspondiente (que ahora sí será una identidad matemática o ecuación de igualdad).

a11·x1 + a12·x2 ≤ b1 a11·x1 + a12·x2 + 1·xs = b1
Restricción de tipo "≥"
En caso de una desigualdad del tipo "≥", también hay que añadir una nueva variable llamada variable de exceso xs (con la condición de no negatividad: xs ≥ 0). Esta nueva variable aparece con coeficiente cero en la función objetivo, y restando en la ecuación correspondiente.

Surge ahora un problema con la condición de no negatividad con esta nueva variable del problema. Las inecuaciones que contengan una desigualdad de tipo "≥" quedarían:

a11·x1 + a12·x2 ≥ b1 a11·x1 + a12·x2 - 1·xs = b1

Al realizar la primera iteración con el método Simplex, las variables básicas no estarán en la base y tomarán valor cero. En este caso la nueva variable xs, tras hacer cero a x1 y x2, tomará el valor -b1 y no cumpliría la condición de no negatividad. Es necesario añadir otra nueva variable xr, llamada variable artificial, que también aparecerá con coeficiente cero en la función objetivo y sumando en la restricción correspondiente. Quedando entonces de la siguiente manera:

a11·x1 + a12·x2 ≥ b1 a11·x1 + a12·x2 - 1·xs + 1·xr = b1
Restricción de tipo "="
Al contrario de lo que cabría pensar, para las restricciones de tipo "=" (aunque ya son identidades) también es necesario agregar variables artificiales xr. Como en el caso anterior, su coeficiente será cero en la función objetivo y aparecerá sumando en la restricción correspondiente.

a11·x1 + a12·x2 = b1 a11·x1 + a12·x2 + 1·xr = b1

En el último caso se hace patente que las variables artificiales suponen una violación de las leyes del álgebra, por lo que será necesario asegurar que dichas variables artificiales tengan un valor 0 en la solución final. De esto se encarga el método de las Dos Fases y por ello siempre que aparezcan este tipo de variables habrá que realizarlo.

En la siguiente tabla se resume según la desigualdad el tipo de variable que aparece en la ecuación normalizada, así como su signo:

Tipo de desigualdad	Tipo de variable que aparece
≥	- exceso + artificial
=	+ artificial
≤	+ holgura

Desarrollando el método Simplex

Una vez estandarizado el modelo puede ocurrir que sea necesario aplicar el método Simplex o el método de las Dos Fases. Véase en la figura la forma de actuación para llegar a la solución del problema modelado.

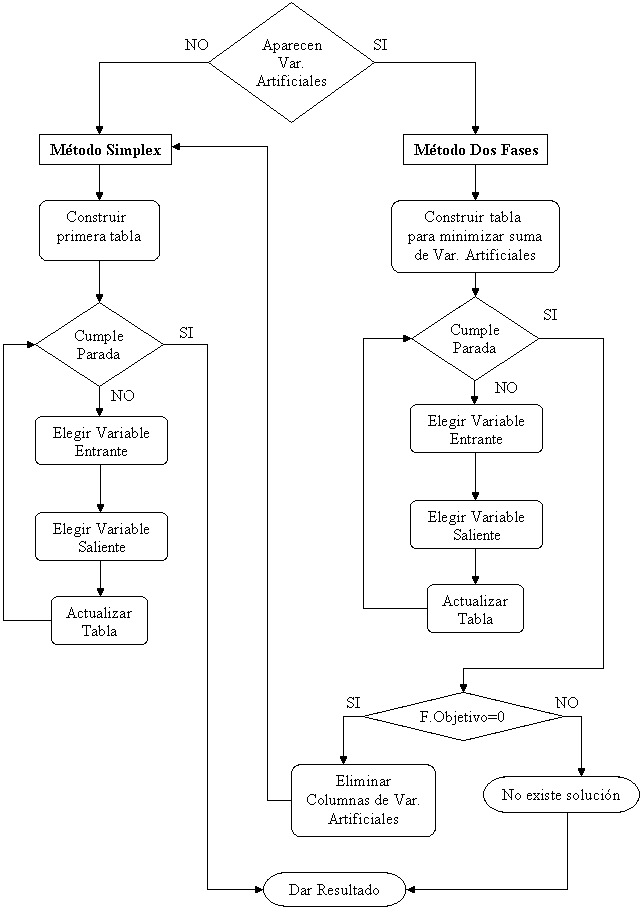
A continuación se explican paso a paso los puntos de cada método, concretando los aspectos a tener en cuenta.

Método Simplex

Construcción de la primera tabla:

Las columnas de la tabla están dispuestas de la siguiente forma: la primera columna de la tabla contiene las variables que se encuentran en la base (o variables básicas), esto es, aquellas que toman valor para proporcionar una solución; la segunda columna recoge los coeficientes que dichas variables básicas tienen en la función objetivo (esta columna es llamada Cb); la tercera muestra el término independiente de cada restricción (P0); a partir de ésta aparece una columna por cada una de las variables de decisión y holgura presentes en la función objetivo (Pj). Para tener una visión más clara de la tabla, se incluye una fila que contiene los títulos de cada una de las columnas.

Sobre esta tabla se agregan dos nuevas filas: una de ellas, que lidera la tabla, donde aparecen los coeficientes de las variables de la función objetivo, y una última fila que recoge el valor la función objetivo y los costes reducidos Zj - Cj.

Los costes reducidos muestran la posibilidad de mejora en la solución Z0. Por este motivo también son llamados valores indicadores.

Se muestra a continuación el aspecto general de la tabla del método Simplex:

Tabla
			C1	C2	...	Cn
Base	Cb	P0	P1	P2	...	Pn
P1	Cb1	b1	a11	a12	...	a1n
P2	Cb2	b2	a21	a22	...	a2n
...	...	...	...	...	...	...
Pm	Cbm	bm	am1	am2	...	amn
Z		Z0	Z1-C1	Z2-C2	...	Zn-Cn

Todos los valores incluidos en la tabla vendrán dados por el modelo del problema salvo los valores de la fila Z (o fila indicadora). Estos se obtienen de la siguiente forma: Zj = Σ(Cbi·Pj) para i = 1..m, donde si j = 0, P0 = bi y C0 = 0, y en caso contrario Pj = aij.

Se observa, al realizar el método Simplex, que en esta primera tabla ocupan la base todas las variables de holgura y por ello (todos los coeficientes de las variables de holgura son 0 en la función objetivo) el valor inicial de Z es cero.

Por este mismo motivo tampoco es necesario realizar los cálculos de los costes reducidos en la primera tabla, pudiéndose determinar directamente como el cambio de signo de los coeficientes de cada variable en la función objetivo, esto es, -Cj.

Condición de parada:
Se cumple la condición de parada cuando la fila indicadora no contiene ningún valor negativo entre los costes reducidos (cuando el objetivo es la maximización), esto es, no existe posibilidad de mejora.

Una vez cumplida la condición de parada, el valor de cada variable que logra la solución óptima se encuentra en la columna P0, indicándose en la base a qué variable correnponde dicho valor. Si una variable no aparece en la base, significa que su valor es cero. De la misma forma el valor óptimo de la función objetivo (Z) se encuentra en la columna P0, fila Z.

Si no se cumple la condición de parada es necesario realizar una iteración más del algoritmo, esto es, determinar la variable que se vuelve básica y la que deja de serlo, encontrar el elemento pivote, actualizar los valores de la tabla y comprobar si se cumple nuevamente la condición de parada.

Es también posible determinar que el problema no se encuentra acotado y su solución siempre resultará mejorable. En tal caso no es necesario continuar iterando indefinidamente y se puede finalizar el algoritmo. Esta situación ocurre cuando en la columna de la variable entrante a la base todos los valores son negativos o nulos.
Elección de la variable que entra a la base:
Cuando una variable se vuelve básica, es decir, entra en la base, comienza a formar parte de la solución. Observando los costes reducidos en la fila Z, se decide que entra a la base la variable de la columna en la que éste sea el de menor valor (o de mayor valor absoluto) entre los negativos.
Elección de la variable que sale de la base:
Una vez obtenida la variable entrante, se determina que sale de la base la variable que se encuentre en aquella fila cuyo cociente P0/Pj sea el menor de los estrictamente positivos (teniendo en cuenta que esta operación se hará únicamente cuando Pj sea superior a 0).
Elemento pivote:
El elemento pivote de la tabla queda marcado por la intersección entre la columna de la variable entrante y la fila de la variable saliente.
Actualización de la tabla:
Las filas correspondientes a la función objetivo y a los títulos permanecerán inalteradas en la nueva tabla. El resto de valores deberán calcularse como se explica a continuación:
- En la fila del elemento pivote cada nuevo elemento se calcula como:
  Nuevo Elemento Fila Pivote = Anterior Elemento Fila Pivote / Pivote.
- En el resto de las filas cada elemento se calcula:
  Nuevo Elemento Fila = Anterior Elemento Fila - (Anterior Elemento Fila en Columna Pivote * Nuevo Elemento Fila Pivote).
De esta forma se consigue que todos los elementos de la columna de la variable entrante sean nulos salvo el de la fila de la variable saliente cuyo valor será 1. (Es análogo a utilizar el método de Gauss-Jordan para resolver sistemas de ecuaciones lineales).

Método de las Dos Fases

El método de las Dos Fases se utiliza cuando aparecen variables artificiales en la forma canónica o estándar del problema. La primera fase trata de resolver el problema auxiliar Z' de minimizar la suma de las variables artificiales y conseguir que sea cero (con objeto de evitar incongruencias matemáticas). Una vez resuelto este primer problema, y siempre y cuando el resultado sea el esperado, se reorganiza la tabla resultante para utilizarla en la segunda fase sobre el problema original.

En caso contrario el problema no es factible, es decir, no tiene solución y no será necesario continuar con la segunda fase.

FASE 1

Esta primera fase es muy similar al método Simplex, con la excepción de la construcción de la primera tabla, además de la necesidad de estudiar el resultado obtenido para determinar si se desarrolla la segunda fase.

En tal caso, la última tabla de esta fase será, con algunas modificaciones, la utilizada como tabla inicial para la segunda fase.

Construcción de la primera tabla:

Se elabora de manera análoga a la tabla inicial del método Simplex, pero con algunas diferencias.

Como se ha comentado, en esta primera fase se resuelve un problema auxiliar (la minimización de la suma de las variables artificiales) con una función objetivo auxiliar. Por lo tanto en la primera fila de la tabla, donde se muestran los coeficientes de las variables de la función objetivo, aparecerán todos los términos a cero excepto los coeficientes de variables artificiales. El valor de cada uno de estos coeficientes es "-1" debido a que se está minimizando la suma de dichas variables (recuerde que minimizar Z' es igual que maximizar (-1)·Z').

La otra diferencia para la primera tabla radica en que ahora sí es necesario calcular la fila Z (o fila indicadora).

Tabla
		C0	C1	C2	...	Cn-k	...	Cn
Base	Cb	P0	P1	P2	...	Pn-k	...	Pn
P1	Cb1	b1	a11	a12	...	a1n-k	...	a1n
P2	Cb2	b2	a21	a22	...	a2n-k	...	a2n
...	...	...	...	...	...	...	...	...
Pm	Cbm	bm	am1	am2	...	amn-k	...	amn
Z		Z0	Z1	Z2	...	Zn-k	...	Zn

Siendo Zj = Σ(Cbi·Pj) - Cj para i = 1..m, donde si j = 0, P0 = bi y C0 = 0, y en caso contrario Pj = aij.

Condición de parada y paso a la fase 2:
La condición de parada es la misma que en el método Simplex normal. Esto es, cuando en la fila indicadora ninguno de los valores de los costes reducidos es negativo (ya que tal y como se ha planteado el objetivo es la maximización de (-1)·Z').

Cumplida la condición de parada es necesario determinar si es posible pasar a la segunda fase para obtener la solución óptima del problema original. Esto se hace observando el resultado obtenido en la primera fase: si su valor es 0, significa que el problema original tiene solución y es posible calcularla, en caso contrario indica que se trata de un problema no factible y no tiene solución.

FASE 2

La segunda fase del método de las Dos Fases se desarrolla exactamente igual que el método Simplex, con la salvedad de que antes de iniciar las iteraciones hay que eliminar las columnas correspondientes a las variables artificiales, y reconstruir la tabla inicial.

Eliminar Columna de variables artificiales:
Si hemos llegado a la conclusión de que el problema original tiene solución, debemos preparar nuestra tabla para la segunda fase. Este paso es muy sencillo, se trata únicamente de eliminar las columnas correspondientes a las variables artificiales.
Construcción de la tabla inicial:
La tabla inicial en este caso se mantiene casi igual a la última tabla de la primera fase. Únicamente habrá que modificar la fila de la función objetivo por la del problema original y calcular nuevamente la fila Z (de la misma forma que en la primera tabla de la fase 1).

A partir de este punto, todas las iteraciones hasta llegar a la solución óptima del problema no presentan ninguna diferencia con el método Simplex.

Identificando casos anómalos y soluciones

Solución óptima: cuando se cumple la condición de parada y no hay variables artificiales en la base con valor positivo (los valores se indican en la columna P0), se ha conseguido la optimización. El valor Z0 actual es la solución óptima del problema, cumpliéndose para las variables que se encuentran en la base. Si se trata de un problema de minimización, el valor óptimo obtenido se multiplicará por "-1".

Infinitas soluciones: cumplida la condición de parada, si alguna variable de decisión no básica tiene un valor 0 en la fila Z, significa que existe otra solución que aporta el mismo valor óptimo para la función objetivo. Es este caso el problema admite infinitas soluciones, estando todas ellas comprendidas dentro del segmento (o porción del plano, región del espacio, etc. dependiendo del número de variables del problema) definido por A·X1 + B·X2 = Z0. Mediante una nueva iteración y haciendo que la variable de decisión que tiene el 0 en la fila Z entre en la base se obtendrá otra solución diferente para el mismo valor óptimo.

Solución ilimitada (no acotada): si toda la columna de la variable que entra a la base tiene todos sus elementos negativos o nulos se trata de problema no acotado, es decir, que tiene solución ilimitada. No hay valor óptimo concreto para la función objetivo sino que a medida que se aumenta el valor de las variables también se incrementa el valor Z sin violar ninguna restricción.

No existe solución: cuando ningún punto satisface todas las restricciones del problema se produce la infactibilidad no existiendo ninguna solución posible para él. En este caso, una vez terminadas todas las iteraciones del algoritmo, existen en la base variables artificiales cuyo valor es superior a cero.

Empate de variable entrante: cuando se produce un empate en la condición de decisión de la variable entrante se puede optar por cualquiera de ellas sin que esto afecte a la solución final. Por contra si influye en el número de iteraciones necesarias para obtener dicha solución. Se aconseja optar a favor de las variables básicas ya que ellas son las que formarán parte de la solución óptima.

Empate de variable saliente: se puede nuevamente optar por cualquiera de ellas. Sin embargo, a fin de no alargar el problema y evitar la entrada en un bucle infinito (caso degenerado), se discrimina a favor de las variables de decisión haciendo que permanezcan en la base. En el caso de estar en la primera fase del método de las Dos Fases, se optará por sacar de la base las variables artificiales.

Curiosidad en la Fase 1: al finalizar la fase 1, si el problema original tiene solución, todas las variables artificiales en la fila indicadora deben tener el valor "1".

¿El elemento pivote puede ser nulo?: No, el elemento pivote siempre será estrictamente positivo ya que únicamente se realizan los cocientes entre valores no negativos y mayores que cero (ante un problema de maximización).